Lk is tangent to circle j at point k. – Line lk is tangent to circle j at point k, a geometric concept that unveils a fascinating interplay between lines and circles. This tangency, characterized by the unique relationship between a line and a curve, holds significant implications in geometry, engineering, and beyond.
As we delve into the properties of tangent lines, we discover their perpendicularity to the radius drawn to the point of tangency, a fundamental characteristic that governs their interaction with circles. Furthermore, we explore the geometric relationships that emerge from this tangency, revealing the connection between the radius length and the distance from the point of tangency to the circle’s center.
Tangency of Line and Circle: Lk Is Tangent To Circle J At Point K.
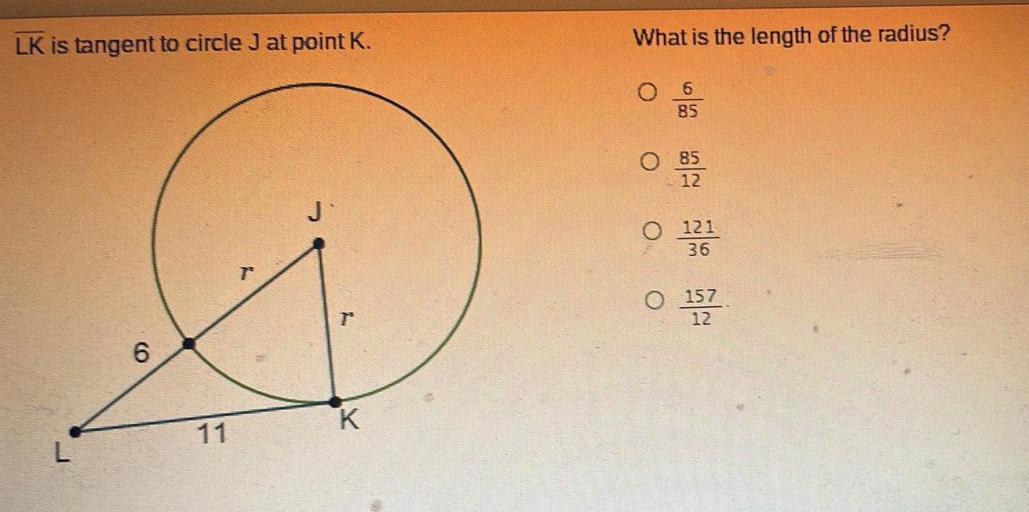
In geometry, a line is tangent to a circle if it intersects the circle at exactly one point. The point of tangency is the point where the line and the circle meet.
The following figure shows a line tangent to a circle at point K:

The line LKis tangent to the circle Jat point K.
Properties of Tangent Lines
Tangent lines to circles possess unique properties that distinguish them from other lines intersecting circles. These properties play a crucial role in geometry and various applications.
Perpendicularity to Radius
One of the fundamental properties of tangent lines is their perpendicularity to the radius drawn to the point of tangency. This means that the tangent line forms a right angle with the radius at the point where it touches the circle.
This perpendicularity can be intuitively understood by considering the motion of a line as it approaches the circle. As the line gets closer to the circle, it becomes increasingly parallel to the tangent line. At the moment of tangency, the line coincides with the tangent line, forming a right angle with the radius drawn to the point of tangency.
The perpendicularity of tangent lines to radii has important implications in various applications, such as geometric constructions, angle measurements, and the design of curves.
Geometric Relationships
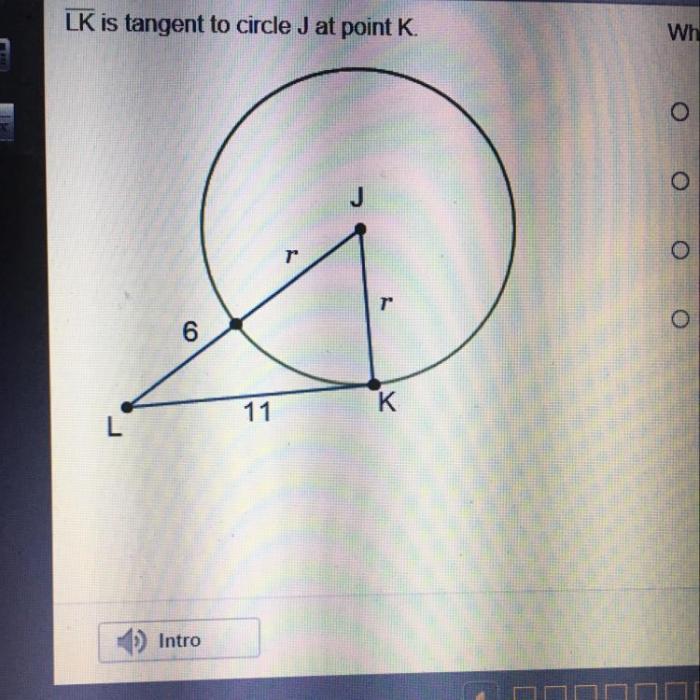
The geometric relationships between the tangent line, the radius, and the circle are crucial in understanding the properties of tangent lines. These relationships provide insights into the lengths and positions of various elements involved.
One of the fundamental relationships is that the radius drawn to the point of tangency is perpendicular to the tangent line. This implies that the radius forms a right angle with the tangent line at the point of contact.
Relationship between Radius Length and Distance to Center, Lk is tangent to circle j at point k.
Another important relationship exists between the length of the radius and the distance from the point of tangency to the center of the circle. This relationship is expressed by the following formula:
$$r^2 = d^2 + h^2$$
where:
- $$r$$ is the radius of the circle
- $$d$$ is the distance from the point of tangency to the center of the circle
- $$h$$ is the length of the perpendicular segment from the point of tangency to the radius
This formula demonstrates that the square of the radius is equal to the sum of the squares of the distance from the point of tangency to the center and the length of the perpendicular segment.
Applications of Tangency
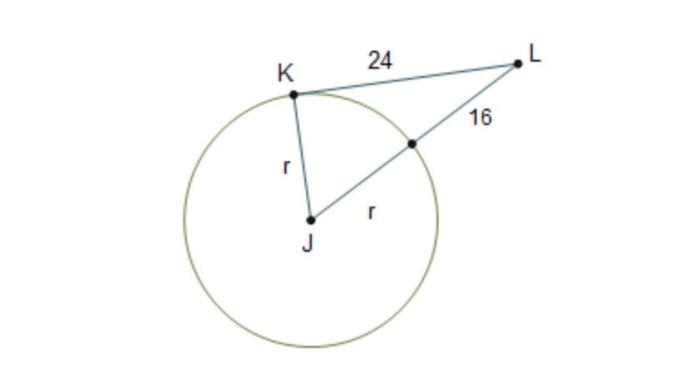
Tangency is a geometric concept with wide-ranging applications in various fields. Tangent lines play a crucial role in geometry, engineering, architecture, and other disciplines, providing valuable insights and solutions to practical problems.
In geometry, tangent lines are used to define and construct various shapes and figures. For example, tangent lines can be used to construct circles that are tangent to other circles or lines. Tangency is also essential in geometric constructions, such as finding the center of a circle or constructing a perpendicular bisector.
Applications in Engineering and Design
In engineering and design, tangent lines are used to analyze and optimize the performance of structures and systems. For example, in mechanical engineering, tangent lines are used to determine the forces and stresses acting on machine components, such as gears and bearings.
In civil engineering, tangent lines are used to design bridges, tunnels, and other structures that require smooth transitions and optimal load distribution.
Significance in Geometric Constructions
Tangency is a fundamental concept in geometric constructions, enabling the creation of precise and accurate figures. By utilizing tangent lines, geometric constructions can be performed with greater accuracy and efficiency. For instance, tangent lines can be used to construct regular polygons, such as squares and hexagons, and to bisect angles or divide line segments into equal parts.
FAQ Resource
What is the definition of a tangent line?
A tangent line is a straight line that intersects a curve at only one point, known as the point of tangency.
How can you determine if a line is tangent to a circle?
A line is tangent to a circle if it is perpendicular to the radius drawn to the point of tangency.
What are the practical applications of tangent lines?
Tangent lines are used in engineering to design optimal shapes, in geometry to solve geometric problems, and in architecture to create precise measurements.